CHUYÊN ĐỀ TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN, CHUYÊN ĐỀ TỈ SỐ LƯỢNG GIÁC LỚP 9

Lớp 1

Tài liệu Giáo viên

Lớp 2

Lớp 2 - kết nối tri thức

Lớp 2 - Chân trời sáng tạo

Lớp 2 - Cánh diều

Tài liệu Giáo viên

Lớp 3

Lớp 3 - liên kết tri thức

Lớp 3 - Chân trời sáng tạo

Lớp 3 - Cánh diều

Tài liệu Giáo viên

Lớp 4

Sách giáo khoa

Sách/Vở bài tập

Tài liệu Giáo viên

Lớp 5

Sách giáo khoa

Sách/Vở bài bác tập

Tài liệu Giáo viên

Lớp 6

Lớp 6 - kết nối tri thức

Lớp 6 - Chân trời sáng tạo

Lớp 6 - Cánh diều

Sách/Vở bài bác tập

Tài liệu Giáo viên

Lớp 7

Lớp 7 - kết nối tri thức

Lớp 7 - Chân trời sáng tạo

Lớp 7 - Cánh diều

Sách/Vở bài bác tập

Tài liệu Giáo viên

Lớp 8

Sách giáo khoa

Sách/Vở bài bác tập

Tài liệu Giáo viên

Lớp 9

Sách giáo khoa

Sách/Vở bài tập

Tài liệu Giáo viên

Lớp 10

Lớp 10 - kết nối tri thức

Lớp 10 - Chân trời sáng sủa tạo

Lớp 10 - Cánh diều

Sách/Vở bài xích tập

Tài liệu Giáo viên

Lớp 11

Sách giáo khoa

Sách/Vở bài tập

Tài liệu Giáo viên

Lớp 12

Sách giáo khoa

Sách/Vở bài bác tập

Tài liệu Giáo viên

gia sư

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Chuyên đề Toán 9Chuyên đề Hình học tập 9Chuyên đề: Hệ thức lượng trong tam giác vuông
Chuyên đề: Đường tròn
Chuyên đề: Góc với đường tròn
Chuyên đề: hình trụ - Hình Nón - Hình Cầu
Chuyên đề Đại Số 9Chuyên đề: Căn bậc hai
Chuyên đề: Hàm số số 1 Chuyên đề: Hệ hai phương trình bậc nhất hai ẩn
Chuyên đề: Phương trình bậc nhì một ẩn số
Tỉ con số giác của góc nhọn
Trang trước
Trang sau

Tỉ con số giác của góc nhọn

A. Phương thức giải

1. Định nghĩa các tỉ con số giác của góc nhọn:

1, sin α = AB/AC

2, cos α = BC/AC

3, tung α = AB/BC

4, cotgα = BC/AB

2. Một vài tính chất của những tỉ số lượng giác

+ cho hai góc α với β phụ nhau. Khi đó:

sin α = cos β

cos α = sin β

tan α = cotg β

cotg α = chảy β

+ mang đến góc nhọn α. Ta có:

0 2B ; CH = a sin2 B

b, Suy ra AB2 = BC.BH ; AH2 = BH.HC

Hướng dẫn giải

a, hội chứng minh:

Xét tam giác vuông ABH, ta có:

AH = sin
B.AB (1)

Xét tam giác vuông ABC, ta có:

AB = BC.cos B = acos B (2)

Từ (1) với (2) ta có:

AH = a sin B cos B

Tương từ bỏ ta có:

+ Xét tam giác vuông ABH: bh = AB.cos B

Xét tam giác vuông ABC: AB = BC.cos B = acos B => bh = a cos2B

+ Xét tam giác vuông ACH: CH = AC.cos C = AC.sin B

Tam giác vuông ABC: AC=BC.sin B=a.sin B => CH = a sin2 B

b, AB2 = a2 cos2B

BC.BH = a.a.cos2B = a2cos2B

=> AB2 = BC.BH

AH2 = a2sin2cos2B

=> AH2 = BH.HC

Bài 2: Giải tam giác trong các trường đúng theo sau( có tác dụng tròn đến chữ số thập phân sản phẩm nhất).(Tức là tìm tất cả các yếu hèn tố chưa chắc chắn của tam giác ABC)

a, Tam giác ABC vuông tại A, biết AB = 3,5; AC = 4,2.

Bạn đang xem: Chuyên đề tỉ số lượng giác của góc nhọn

b, Tam giác ABC vuông tại A, biết ∠B = 50o ; AB = 3,7.

Hướng dẫn giải

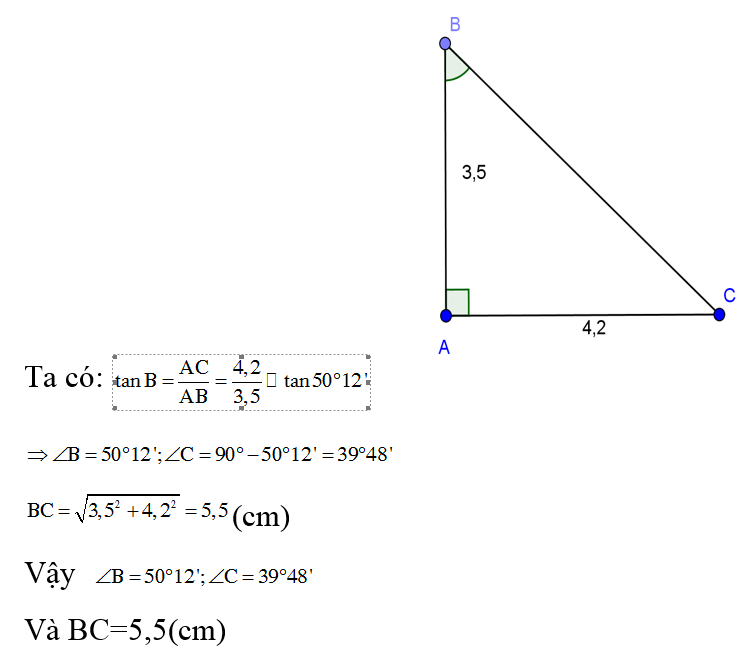
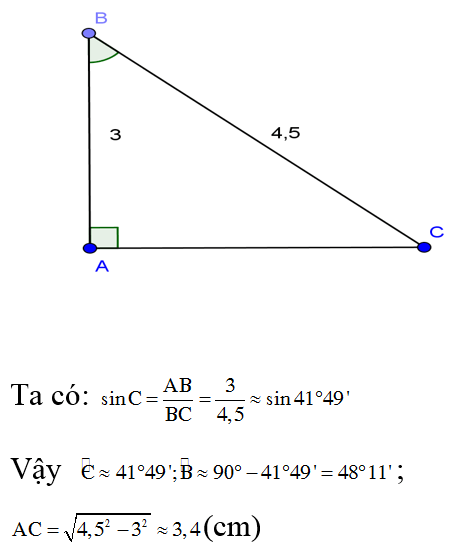
Bài 3: Giải tam giác ABC, biết ∠B = 65o; ∠C = 40o cùng BC = 4,2 cm.

Hướng dẫn giải

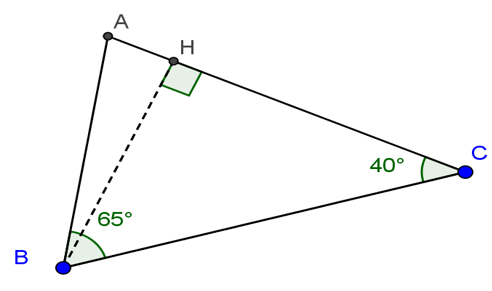
Ta có: ∠A = 180o - (65o + 45o) = 75o

Vẽ bh ⊥ AC

+ Xét tam giác vuông HBC vuông trên H, theo hệ thức về cạnh cùng góc trong tam giác vuông, ta có:

BH = BC.sin C = 2,7 (cm)

Và CH = BH.cotg C (1)

+ Xét tam giác vuông ABH tại H, theo hệ thức về cạnh cùng góc vào tam giác vuông ta có:

BH = AB.sin A => AB = BH/sin
A = 2,8 (cm) với AH = BH.cotg A (2)

Từ (1) và (2) ta có:

AC = AH+CH = BH.cotg
A + BH.cotg
C = BH(Cotg A+Cotg C)= 3,9(cm)

Vậy ∠A = 75o; AB = 2,8(cm); AC = 3,9(cm).

Tham khảo thêm những Chuyên đề Toán lớp 9 khác:

ĐỀ THI, GIÁO ÁN, KHÓA HỌC DÀNH mang lại GIÁO VIÊN VÀ PHỤ HUYNH LỚP 9

Bộ giáo án, bài xích giảng powerpoint, đề thi dành cho giáo viên cùng khóa học dành cho phụ huynh trên https://tailieugiaovien.com.vn/ . Cung cấp zalo Viet
Jack Official

Với siêng đề Tỉ con số giác của góc nhọn (2022) - Toán 9 mới nhất được biên soạn bám sát đít chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.

1. Quan niệm tỉ con số giác của một góc nhọn

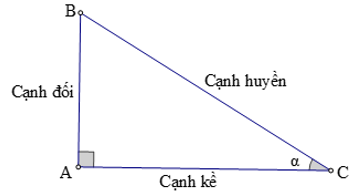
+ Tỉ số thân cạnh đối cùng cạnh huyền được call làsincủa góc α, kí hiệu là sin α.

+ Tỉ số thân cạnh kề cùng cạnh huyền được điện thoại tư vấn làcôsincủa góc α, kí hiệu là cos α.

+ Tỉ số thân cạnh đối với cạnh kề được hotline làtangcủa góc α, kí hiệu là tan α.

+ Tỉ số giữa cạnh kề với cạnh đối được gọi làcôtangcủa góc α, kí hiệu là cot α.

Ví dụ 1.Cho tam giác ABC có
C^=α.

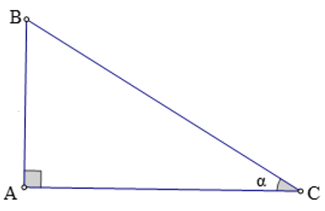
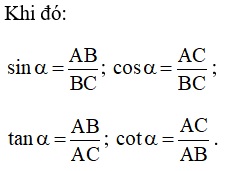
Nhận xét:Nếu α là một trong những góc nhọn thì:

0 0; cot α > 0.

Ví dụ 2.Cho tam giác ABC có
C^=α

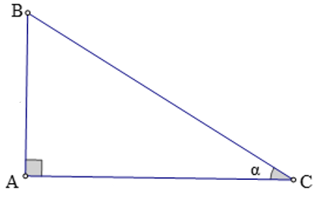
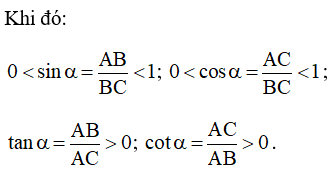
Chú ý:Nếu hai góc nhọn α và β gồm sin α = sin β (hoặc cos α = cos β, hoặc tung α = chảy β, hoặc cot α = cot β) thì α = β do chúng là nhì góc khớp ứng của nhị tam giác vuông đồng dạng.

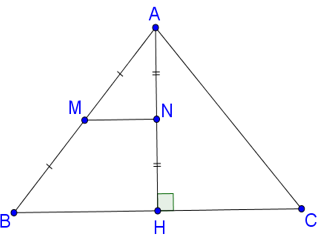
Ví dụ 3.Cho tam giác ABC bao gồm AB = AC, con đường cao AH. MN là mặt đường trung bình của tam giác ABH. Hội chứng minh
AMN^=C^.

Lời giải:

Vì AH là con đường cao của ∆ABC nên
AH⊥BChay
AH⊥BH(1)

Mà MN là con đường trung bình của ∆AMN nên:

+ AB = 2AM; AH = 2AN.

+ MN // bảo hành (2)

Từ (1) với (2) suy ra
MN⊥BH(tính hóa học từ vuông góc đến tuy vậy song).

2. Tỉ con số giác của nhị góc phụ nhau

Định lí.Nếu nhì góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Ví dụ 4.Cho tam giác ABC vuông trên A có
B^=α;  C^=β.

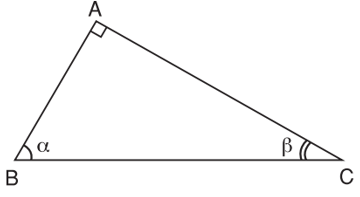
Khi đó, α + β = 90° (trong tam giác vuông nhì góc nhọn phụ nhau).

Ta có: sin α = cos β; cos α = sin β; tan α = cot β; cot α = chảy β.

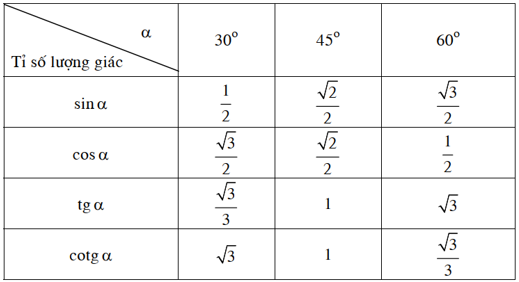
Bảng lượng giác của một số trong những góc sệt biệt:

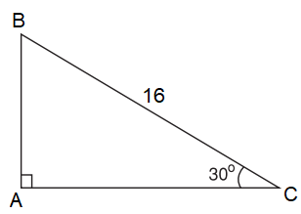
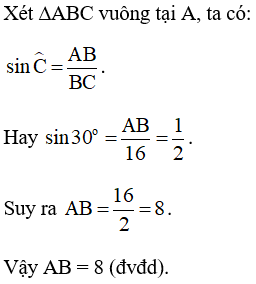
Chú ý:Từ nay khi viết những tỉ số lượng giác của một góc nhọn trong tam giác, ta quăng quật kí hiệu " ^ " đi.

Ví dụ 6.Góc A là góc nhọn thì ta viết sin A ráng chosin
A^.

Xem thêm: Các Hình Dạng Của Cô Bé Và Những Hình Dạng Của Cô Bé Phổ Biến Nhất Hiện Nay

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1:Cho tam giác MNP vuông tại M. Khi đó

bằng

Lời giải:

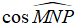
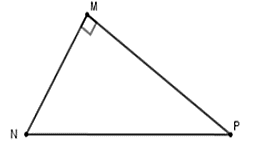
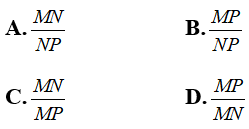
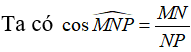
Chọn câu trả lời A

Câu 2:Cho α là góc nhọn bất kỳ. Chọn xác định đúng.

Lời giải:

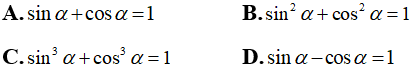
Cho α là góc nhọn bất kỳ, lúc ấy sin2α + cos2α = 1

Chọn đáp án B

Câu 3:Cho α là góc nhọn bất kỳ. Chọn xác minh sai.

Lời giải:

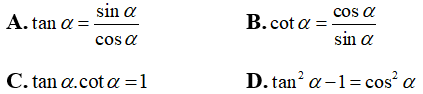
Cho α là góc nhọn bất kỳ, lúc đó

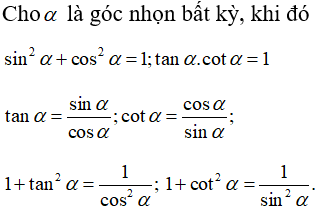
Chọn lời giải D

Câu 4:Cho α cùng β là góc nhọn bất kỳ thỏa mãn α + β = 90° . Chọn khẳng định đúng.

A.α + β = 90°

B.tanα = cotβ

C.tanα = cosα

D.tanα = tanβ

Lời giải:

Với hai góc α cùng β mà lại α + β = 90 °

sinα = cosβ; cosα = sinβ

tanα = cotβ ; cotα = tanβ

Chọn câu trả lời B

Câu 5:Cho tam giác ABC vuông trên c tất cả BC = 1,2 cm, AC = 0,9 cm . Tính những tỉ con số giác sin
B; cos
B

Lời giải:

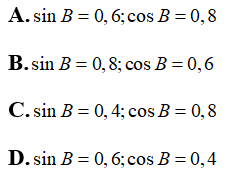
Chọn câu trả lời A

Câu 6:Cho tam giác ABC vuông tại A, AB = 30 cm. Biết tung B = 8/15. Tìm xác minh sai trong các khẳng định sau :

Lời giải:

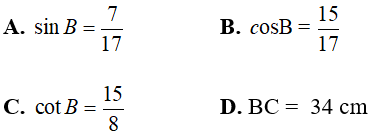
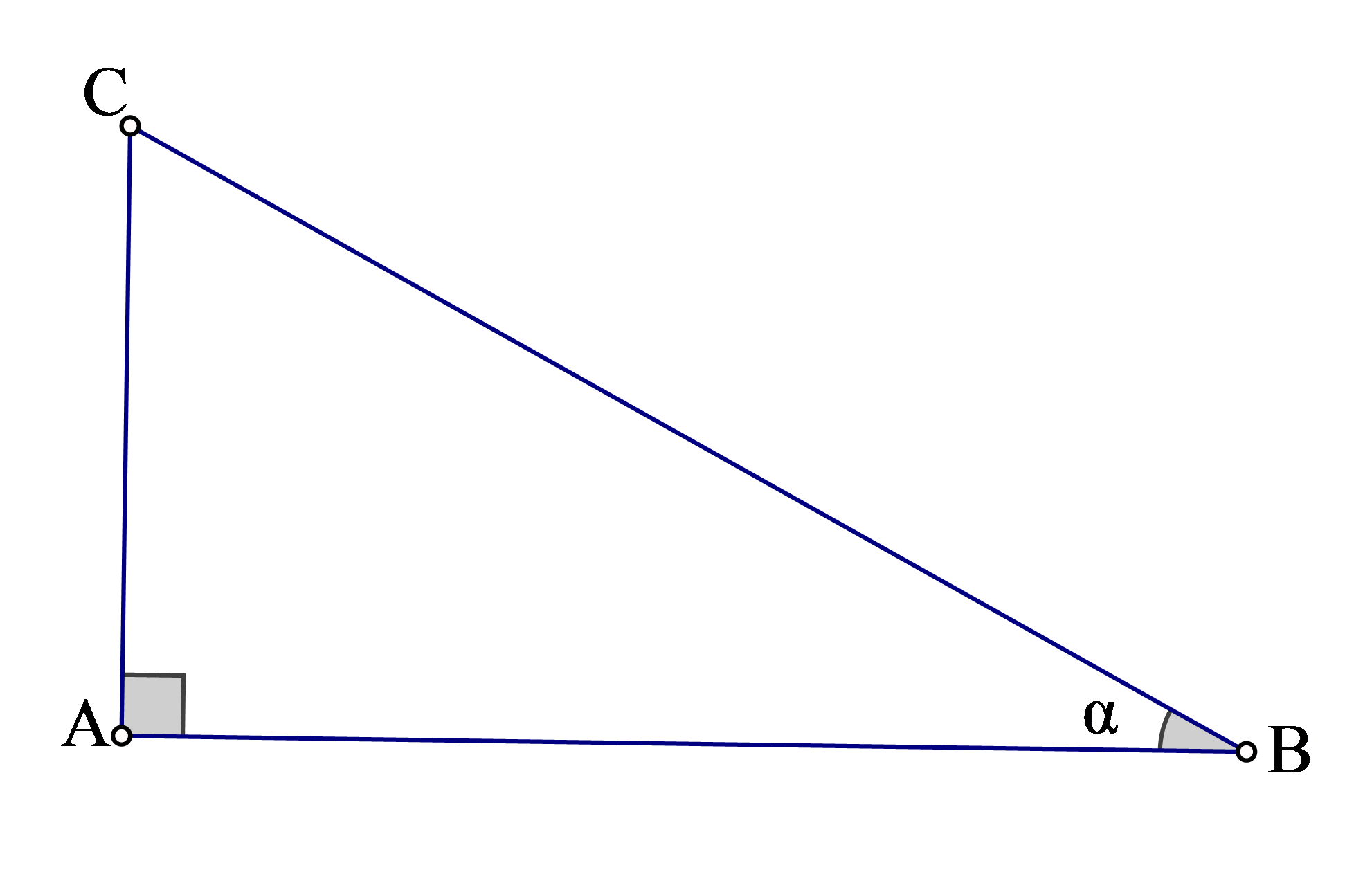
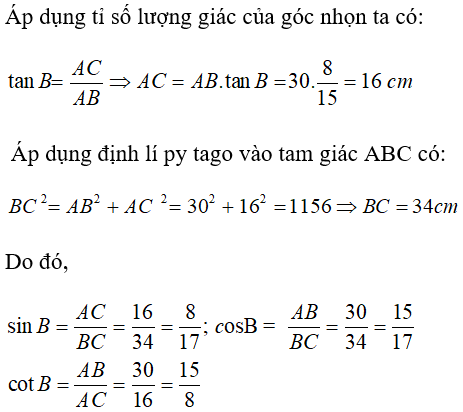
Chọn lời giải A.

Câu 7:Cho tam giác ABC vuông trên A. Tính

Lời giải:

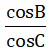
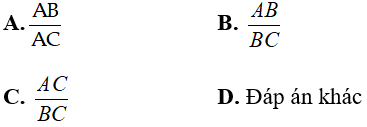
Áp dụng tỉ con số giác của góc nhọn vào tam giác vuông ta có:

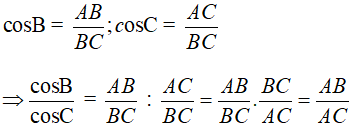
Chọn đáp án A.

Câu 8:Cho tam giác ABC vuông tại A có đường trung con đường ứng với cạnh huyền AM = 10 cm; AB = 16 centimet . Tính cot B?

Lời giải:

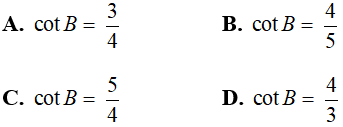
Do tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền nên:

Chọn câu trả lời D.

Câu 9:Cho Δ ABC vuông trên A, con đường cao AH. Biết AB = 13cm và bh = 5 cm. Tính tung C

Lời giải:

Áp dụng định lí Pytago vào tam giác ABH vuông trên H ta có:

AH2+ BH2= AB2

&h
Arr; AH2= AB2- BH2= 132- 52= 144

&h
Arr; AH = 12cm

Áp dụng tỉ con số giác của nhọn trong tam giác vuông ABH ta có:

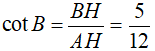
Do tam giác BAC là tam giác vuông bắt buộc hai góc B với C là 2 góc phụ nhau.

Suy ra:

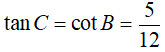
Chọn câu trả lời B.

Câu 10:Cho tam giác ABC vuông trên A bao gồm AC = 8cm cùng góc C = 60°. Tính diện tích tam giác ABC .

A.32 cm2

B.16√3 cm2

C.16 cm2

D.32√3 cm2

Lời giải: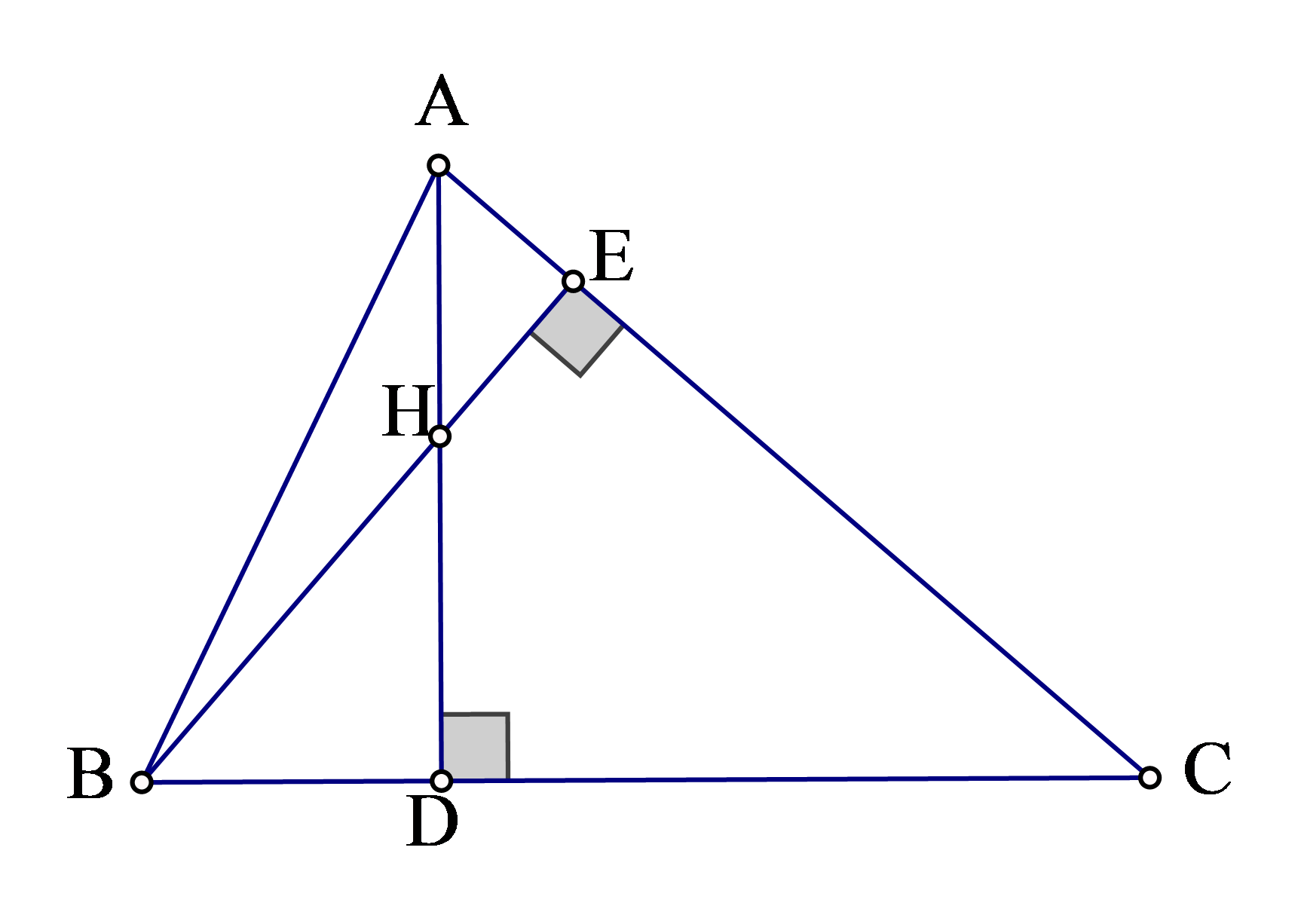

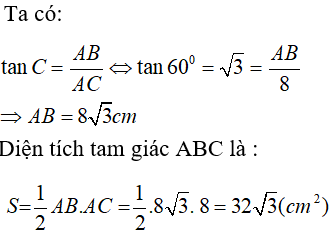
Chọn câu trả lời D.

II. Bài tập từ bỏ luận gồm lời giải

Câu 1:Biết sinα = 5/13. Tính cosα, tanα cùng cotα.

Lời giải:

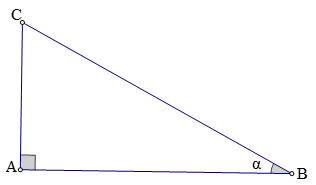
Xét ΔABC vuông tại A.

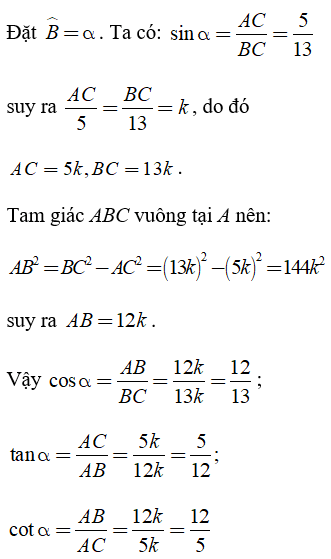
Câu 2:Biết sinα.cosα = 12/25. Tính sinα, cosα.

Lời giải:

Biết sinα.cosα = 12/25. Để tính sinα,cosα ta nên tính sinα + cosα rồi giải phương trình cùng với ẩn là sinα hoặc cosα.

Ta có:

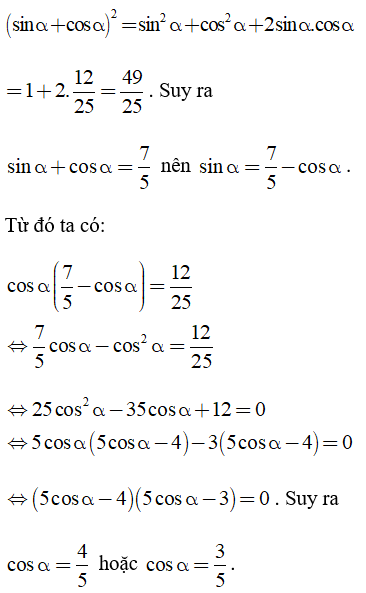
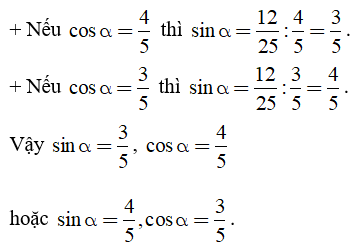
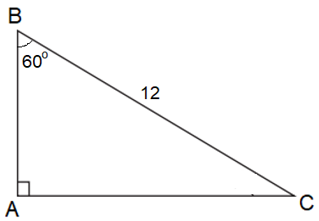
Câu 3:Cho tam giác ABC vuông tại A có
ABC^=60ovà BC = 12. Tính độ lâu năm cạnh AC.

Lời giải:

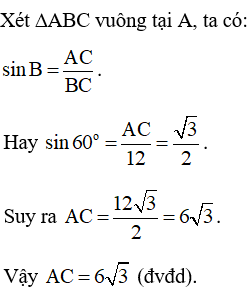
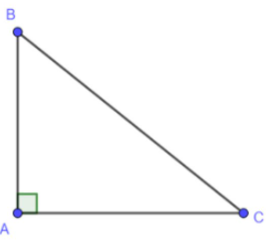
Câu 4:Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng tỏ rằng: cùng với góc nhọnαtùy ý, ta có: sin2α+ cos2α=1.

Lời giải:

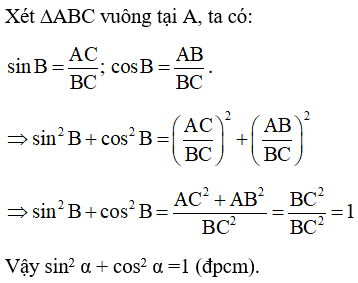
Câu 5: Biếtsinα=35. Tính cosα, tanαvà cotα.

Lời giải:

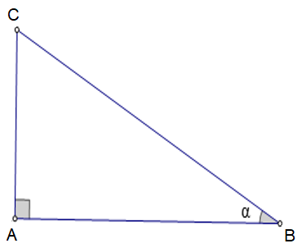
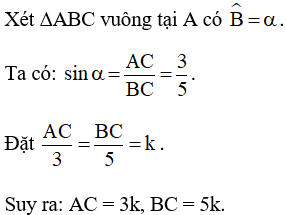
Áp dụng định lý Py-ta-go vào ∆ABC vuông tại A, ta có:

BC2= AB2+ AC2

AB2= BC2− AC2

AB2= (5k)2– (3k)2= 25k2– 9k2= 16k2.

Suy ra: AB = 4k.

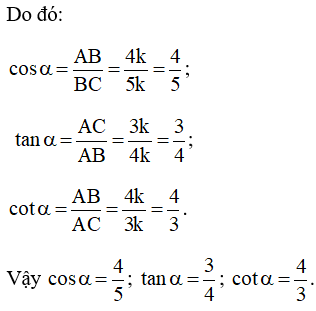
Câu 6:Vẽ một tam giác vuông tất cả một góc nhọn bằng40orồi viết những tỉ số lượng giác của góc40o.

Lời giải:

Vẽ tam giác ABC vuông trên A, có:

B^=40o , AB = c, AC = b, BC = a

Ta có những tỉ con số giác của góc
B^=40olà:

sin
B=ACBC⇒sin40o=bacos
B=ABBC⇒cos40o=catan
B=ACAB⇒tan40o=bccot
B=ABAC⇒cot40o=cb

Câu 7:Cho tam giác ABC vuông tại A. Chứng minh rằng:ACAB=sin
Bsin
C.

Lời giải:

Xét tam giác ABC vuông trên A

Ta có:

sin
B=ACBC⇒AC=sin
B.BCsin
C=ABBC⇒AB=sin
C.BC⇒ACAB=sin
B.BCsin
C.BC=sin
Bsin
C

(điều cần được chứng minh)

Câu 8:Cho tam giác ABC vuông tại A,B^=30o, BC = 8cm. Hãy tính cạnh AB (làm tròn đến chữ số thập phân lắp thêm ba), biết rằngcos30o≈0,866

Lời giải:

Xét tam giác ABC vuông tại A

B^=30o

BC = 8cm

Ta có:

cos
B=ABBC⇒AB=cos
B.BC=cos30o.8≈0,866.8≈6,928 (cm)

Câu 9:Cho tam giác ABC vuông tại A, AB = 6cm,B^=α(h.9). Biếttanα=512, hãy tính

a) Cạnh AC

b) Cạnh BC

Lời giải:

a)

Xét tam giác ABC vuông trên A

AB = 6cm,B^=α

Ta có:

tan
B=ACAB⇒AC=tan
B.AB=tanα.6=512.6=2,5 (cm)

b)

Xét tam giác ABC vuông trên A

Áp dụng định lí Py-ta-go ta có:

BC2=AB2+AC2=62+(2,5)2=42,25

⇒BC=42,25=6,5(cm)

Câu 10:Cho tam giác ABC vuông tại A, trong những số ấy AB = 6cm, AC = 8cm. Tính các tỉ số lượng giác của góc B, từ kia suy ra những tỉ con số giác của góc C.

Lời giải:

Xét tam giác ABC vuông trên A

AB = 6cm, AC = 8cm

Áp dụng định lí Py-ta-go ta có:

BC2=AB2+AC2=62+82=100⇒BC=100=10 (cm)

Ta có các tỉ số lượng giác của góc B.

sin
B=ACBC=810=45cos
B=ABBC=610=35tan
B=ACAB=86=43cot
B=ABAC=68=34

Có
A^=90o⇒B^+C^=90o

Do đó, góc B và góc C là nhì góc phụ nhau phải ta có:

cos
C=sin
B=45sin
C=cos
B=35cot
C=tan
B=43tan
C=cot
B=34

III. Bài bác tập vận dụng

Câu 1:Cho tam giác ABC vuông tại A gồm BC = 9cm; AC = 5cm. Tính tỉ con số giác tung C (làm tròn cho chữ số thập phân đồ vật 1)

Câu 2:Cho tam giác ABC vuông trên A, con đường cao AH bao gồm AB = 13cm, bảo hành = 0,5dm. Tính tỉ con số giác sin
C (làm tròn đến chữ số thập phân sản phẩm công nghệ 2)

Câu 3:Cho tam giác ABC vuông trên A, đường cao AH có AC = 15cm, CH = 6cm. Tính tỉ số lượng giác cos B.

Câu 4:Cho tam giác ABC vuông trên A, con đường cao AH bao gồm CH = 4cm, bảo hành = 3cm. Tính tỉ con số giác cos C (làm tròn cho chữ số thập phân vật dụng 2)

Câu 5: Cho tam giác nhọn ABC hai tuyến đường cao AD với BE giảm nhau tại H. Biết HD:HA = 1:2 . Minh chứng rằng tg
B.tg
C = 3 .

Câu 6: Cho tam giác ABC nhọn. Gọi a, b, c theo lần lượt là độ dài những cạnh đối lập với các đỉnh A, B, C. Chứng minh rằng:

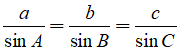
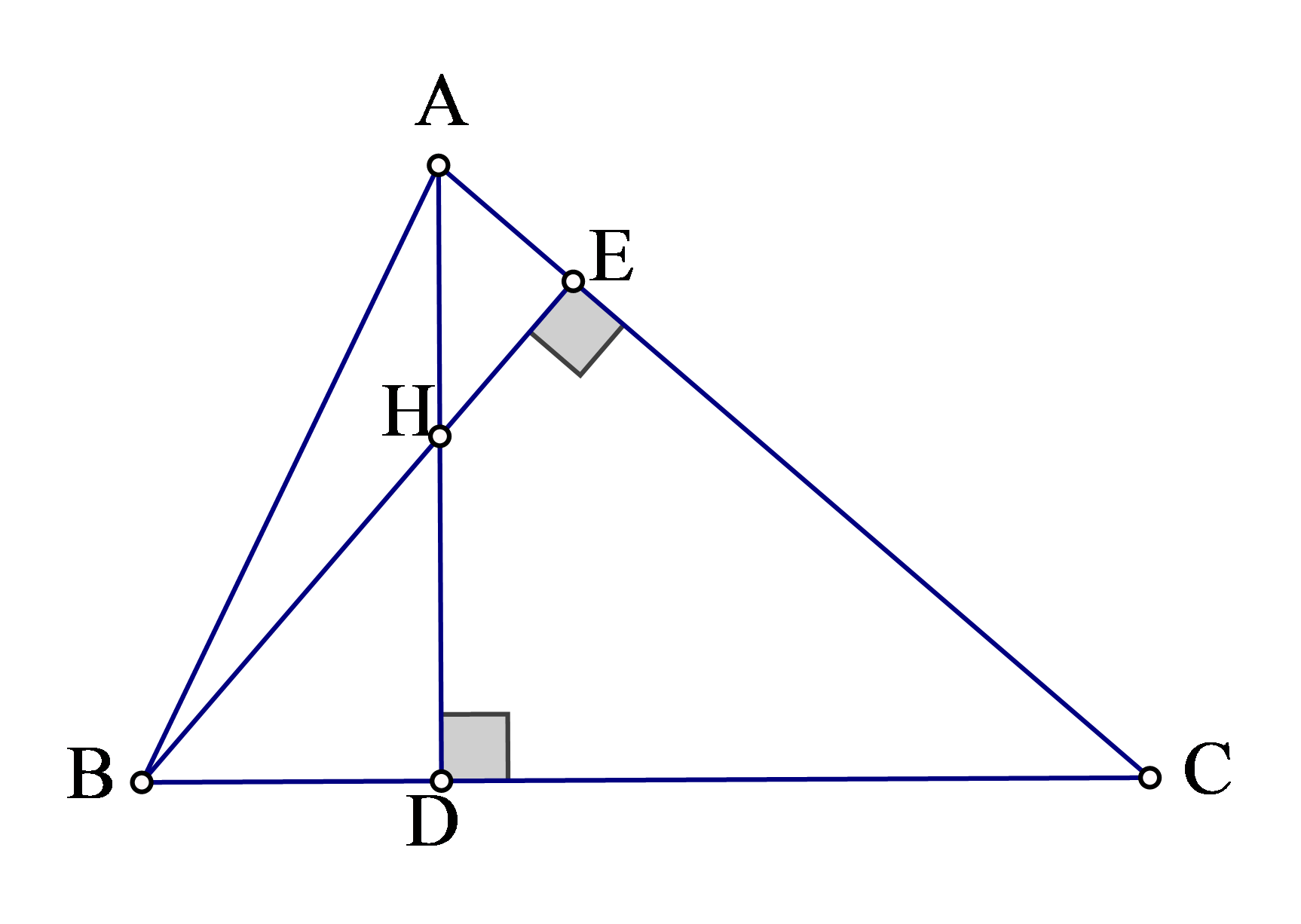
Câu 7:Cho tam giác ABC vuông tại A. Biết AB=6cm, BC=10cm. Tínhsin
ABC^,sin
ACB^,cos
ABC^,cos
ACB^.

Câu 8:Cho tam giác ABC vuông trên A. Bao gồm AB=3cm, AC=4cm. Tínhtan
ABC^,tan
ACB^,cot
ABC^,cot
ACB^.

Câu 9:Cho tam giác ABC. Bao gồm đường cao AH ứng với cạnh BC. AH=5cm, AB=7cm. Tínhsin
ABH^, cos
ABH^